カオスとアトラクタ

1. プログラムの概要

chaos - 奇妙なアトラクタの値を出力する

bifur - 奇妙なアトラクタの振舞いを画面に表示する (Cのみ)

2. C

2.1. chaos

/*
 * オリジナルの出典「C言語による最新アルゴリズム事典」奥村晴彦著 - P28
 * インデントは変更してあります。
 * 他にも、メッセージや変数名や処理を変更している場合があります。
 */

#include <stdio.h>

int main()
{
    int i;
    double p, k;

    printf("factor? ");
    scanf("%lf", &k);

    printf("initial value? ");
    scanf("%lf", &p);

    for (i = 1; i <= 100; i++)
    {
        printf("%10.3f", p);
        if (i % 4 == 0)
        {
            printf("\n");
        }
        p += k * p * (1 - p);
    }
}

2.2. bifur

グラッフィクスのライブラリとして、raylibを使いました。座標単位を変換するためのコードも追加してあります。

コンパイル例：

$ gcc bifur.c -o bifuer -L/usr/loca/lib64 -lraylib -lm

/*
 * オリジナルの出典「C言語による最新アルゴリズム事典」奥村晴彦著 - P29
 * インデントは変更してあります。
 * 他にも、メッセージや変数名や処理を変更している場合があります。
 */

#include <raylib.h>
#include <stdio.h>
#include <stdlib.h>

double wx1, wy1, wx2, wy2, fact_x, fact_y;

void reset_window_coord()
{
    fact_x = GetScreenWidth() / (wx2 - wx1);
    fact_y = GetScreenHeight() / (wy2 - wy1);
}

void put_pixel(double x, double y, Color color)
{
    int sx = fact_x * (x - wx1);
    int sy = fact_y * ((wy2 - wy1) - (y - wy1));
    DrawPixel(sx, sy, color);
}

int main()
{
    int i;
    double k, p, dk, kmin, kmax, pmin, pmax, temp;

    printf("kmin? ");
    scanf("%lf", &kmin);
    printf("kmax? ");
    scanf("%lf", &kmax);
    printf("pmin? ");
    scanf("%lf", &pmin);
    printf("pmax? ");
    scanf("%lf", &pmax);

    if (kmin == kmax || pmin == pmax)
    {
        fprintf(stderr, "invalid parameters\n");
        return EXIT_FAILURE;
    }

    if (kmin > kmax)
    {
        temp = kmin;
        kmin = kmax;
        kmax = temp;
    }

    if (pmin > pmax)
    {
        temp = pmin;
        pmin = pmax;
        pmax = temp;
    }

    wx1 = kmin;
    wx2 = kmax;
    wy1 = pmin;
    wy2 = pmax;

    InitWindow(600, 500, "bifur");
    SetTargetFPS(30);

    dk = (kmax - kmin) / (GetScreenWidth() - 1);
    reset_window_coord();

    while (!WindowShouldClose())
    {
        BeginDrawing();

        ClearBackground(BLACK);

        for (k = kmin; k <= kmax; k += dk)
        {
            p = 0.3;
            for (i = 1; i <= 50; i++)
            {
                p += k * p * (1 - p);
            }
            for (i = 51; i <= 100; i++)
            {
                if (p >= pmin && p <= pmax)
                {
                    put_pixel(k, p, WHITE);
                }
                p += k * p * (1 - p);
            }
        }

        EndDrawing();
    }

    CloseWindow();
}

入力値を 1.5 3 0 1.5 とした場合、次のような結果になります。

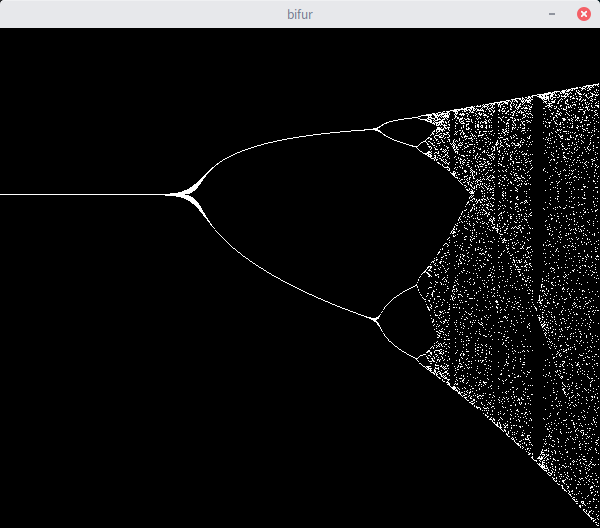
bifur program output screenshot

図1: bifurによる出力

3. Emacs Lisp

(let (i
      (k (read-number "factor? "))
      (p (read-number "initial value? ")))
  (with-output-to-temp-buffer "*chaos*"
    (setq i 1)
    (while (<= i 100)
      (princ (format "%10.3f" p))
      (when (= (% i 4) 0)
        (princ "\n"))
      (setq p (+ p (* k p (- 1 p))))
      (setq i (1+ i)))))

4. Bash

#!/bin/bash

function fmath {
    echo "scale=10; $@" | bc
}

read -p "factor? " k
read -p "initial value? " p

for i in {1..100}
do
    printf "%10.3f" $p
    if [ $(( $i % 4 )) -eq 0 ]
    then
        printf "\n"
    fi
    p=$(fmath "$p + $k * $p * (1 - $p)")
done

5. Fish

#!/usr/bin/fish

read -P "factor? " k
read -P "initial value? " p

for i in (seq 100)
    printf "%10.3f" $p
    if test (math $i % 4) -eq 0
        printf "\n"
    end
    set p (math -s15 "$p + $k * $p * (1 - $p)")
end