黄金分割法

1. プログラムの概要

goldsect - 黄金分割法で与えられた区間で関数の最小値を求める

2. C

/*
 * オリジナルの出典「C言語による最新アルゴリズム事典」奥村晴彦著 - P19
 * インデントは変更してあります。
 * 他にも、メッセージや変数名や処理を変更している場合があります。
 */

#include <math.h>
#include <stdio.h>

double goldsect(double a, double b, double tolerance, double (*f)(double x))
{
    double const r = 2.0 / (3 + sqrt(5)); /* 1 / φ^2 */
    double c, d, fc, fd, t, u;

    /* make sure a < b */
    if (a > b)
    {
        t = a;
        a = b;
        b = t;
    }

    u = r * (b - a);
    c = a + u;
    d = b - u;
    fc = f(c);
    fd = f(d);

    while (1)
    {
        if (fc > fd)
        {
            a = c;
            c = d;
            fc = fd;
            d = b - r * (b - a);
            if (d - c <= tolerance)
            {
                return c;
            }
            fd = f(d);
        }
        else
        {
            b = d;
            d = c;
            fd = fc;
            c = a + r * (b - a);
            if (d - c <= tolerance)
            {
                return d;
            }
            fc = f(c);
        }
    }
}

double f(double x)
{
    return x * x;
}

int main()
{
    double xmin = goldsect(-10, 10, 1e-6, f);
    printf("(x, y) = (%lf, %lf)\n", xmin, f(xmin)); /* expects (0, 0) */

    xmin = goldsect(4, 20, 1e-6, f);
    printf("(x, y) = (%lf, %lf)\n", xmin, f(xmin)); /* expects (4, 16) */
}

イメージは次のようになります。

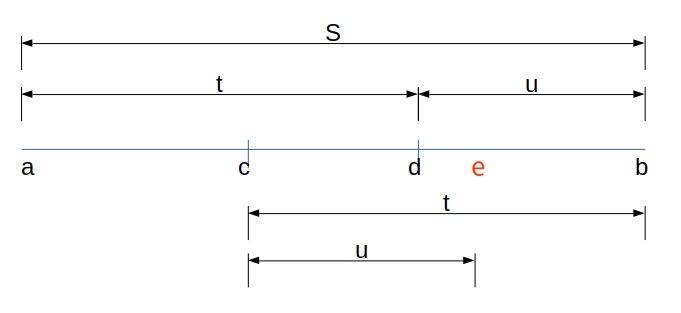
sections with golden ratio

図1: 黄金比による分割

\(s : t = t : u\) になるような比率で、区間を分割しながらどんどん範囲を狭めていきます。

ここで \(u = s - t\) なので、上式に代入すると \(s : t = t : (s - t)\) となり、これを解いてみます。

\(s(s - t) = t^2\)

\(s^2 - st - t^2 = 0\)

\(\frac{s^2}{t^2} - \frac{s}{t} - 1 = 0\)

\(\frac{s}{t} = \frac{1 \pm \sqrt{5}}{2}\)

\(s > 0\) かつ \(t > 0\) なので

\(\frac{s}{t} = \frac{1 + \sqrt{5}}{2} = 1.618033988749...\)

この比率は黄金比と呼ばれ、記号 \(\phi\) で表わされることが多いです。

先のプログラムで double const r = 2.0 / (3 + sqrt(5)); としているところに黄金比が含まれています。値が違っているのは、黄金比の逆数の二乗をとっているからです (\(\frac{1}{\phi^2}\))。なぜそうなっているかというと、ちょっとややこしいです。今、欲しいのはcとdのx値です。そして \(c = a + u\) と \(d = b - u\) となっています。ここで \(u\) を \(\phi\) で表わすことを考えてみます。

\(\frac{s}{t} = \phi\)

\(t = \frac{s}{\phi}\)

となります。

同様に、

\(\frac{t}{u} = \phi\)

\(u = \frac{t}{\phi}\)

となります。そして、先の \(t = \frac{s}{\phi}\) を代入してやります。

\(u = \frac{s / \phi}{\phi} = \frac{s}{\phi^2}\)

となり \(s\) は \(a - b\) なので、

\(c = a + \frac{b - a}{\phi^2}\)

\(d = b - \frac{b - a}{\phi^2}\)

という結果を得ることができます。

3. Emacs Lisp

(defun goldsect (a b tolerance f)
  (let ((r (/ 2.0 (+ 3 (sqrt 5))))
        c d fc fd temp u)

    ;; make sure a < b
    (when (> a b)
      (setq temp a
            a b
            b temp))

    (setq u (* r (- b a))
          c (+ a u)
          d (- b u)
          fc (funcall f c)
          fd (funcall f d))

    (while (> (- d c) tolerance)
      (cond ((> fc fd)
             (setq a c
                   c d
                   fc fd
                   d (- b (* r (- b a)))
                   fd (funcall f d))
             )
            (t
             (setq b d
                   d c
                   fd fc
                   c (+ a (* r (- b a)))
                   fc (funcall f c)))))
    c))

(defun foo (x)
  (+ (* x x) 30))

(let ((xmin (goldsect -10 10 1e-10 'foo)))
  (message "(%f, %f)" xmin (foo xmin))) ;expects (0, 30)

4. Bash

#!/bin/bash

function fmath {
    echo "scale=10; $@" | bc
}

function goldsect {
    a=$1
    b=$2
    tolerance=$3
    f=$4

    # make sure a < b
    if [ $a -gt $b ]
    then
        t=$a
        a=$b
        b=$t
    fi

    r=$(fmath "2.0 / (3 + sqrt(5))")
    u=$(fmath "$r * ($b - $a)")
    c=$(fmath $a + $u)
    d=$(fmath $b - $u)
    fc=$($f $c)
    fd=$($f $d)

    while true
    do
        if [ $(fmath "$fc > $fd") -eq 1 ]
        then
            a=$c
            c=$d
            fc=$fd
            d=$(fmath "$b - $r * ($b - $a)")
            if [ $(fmath "$d - $c <= $tolerance") -eq 1 ]
            then
                echo $c
                return 0
            fi
            fd=$($f $d)
        else
            b=$d
            d=$c
            fd=$fc
            c=$(fmath "$a + $r * ($b - $a)")
            if [ $(fmath "$d - $c <= $tolerance") -eq 1 ]
            then
                echo $d
                return 0
            fi
            fc=$($f $c)
        fi
    done
}

function foo {
    echo "$1 * $1" | bc
}

xmin=$(goldsect -10 10 0.0000001 foo)
echo $xmin $(foo $xmin)

5. Fish

#!/usr/bin/fish

function fmath
    math -s15 "$argv"
end

function goldsect
    set a $argv[1]
    set b $argv[2]
    set tolerance $argv[3]
    set f $argv[4]

    # make sure a < b
    if test $a -gt $b
        set t $a
        set a $b
        set b $t
    end

    set r (fmath "2.0 / (3 + (sqrt 5))")
    set u (fmath "$r * ($b - $a)")
    set c (fmath $a + $u)
    set d (fmath $b - $u)
    set fc ($f $c)
    set fd ($f $d)

    while true
        if test $fc -gt $fd
            set a $c
            set c $d
            set fc $fd
            set d (fmath "$b - $r * ($b - $a)")
            if test (fmath "$d - $c") -le $tolerance
                echo $c
                return 0
            end
            set fd ($f $d)
        else
            set b $d
            set d $c
            set fd $fc
            set c (fmath "$a + $r * ($b - $a)")
            if test (fmath "$d - $c") -le $tolerance
                echo $d
                return 0
            end
            set fc ($f $c)
        end
    end
end

function foo
    echo (fmath "$argv[1] * $argv[1]")
end

set xmin (goldsect -10 10 0.0000001 foo)
printf "(%f, %f)\n" $xmin (foo $xmin) # expects (0, 0)

set xmin (goldsect -5 -10 0.0000001 foo)
printf "(%f, %f)\n" $xmin (foo $xmin) # expects (-5, 25)