ブロック崩しを作る (3)
前回ブロックを表示するところまで作りました。今回やることは主に衝突判定です。
やることを全部リストにすると以下のようになります。
- 壁を作る。
- ボールを動かす。
- ボールが壁に当たったら跳ね返るようにする。
- ボールがパドルに当たったら跳ね返るようにする。
- ボールがブロックに当たったら跳ね返るようにする。
- ボールがブロックに当たったらブロックが消えるようにする。
順番にやっていきたいと思います。
壁を作る
前回作ったやつは壁がなかったので作っておきます。別になくても画面端でボールが跳ね返るようにししてもいいのですが、見栄えと衝突の判定を楽にするために作っておきます。
壁もまたブロックやボールやパドルと同じBrick構造体を使うことにします。タグに"wall"とつけておきます。Bricks構造体は次のようになっています。
struct Brick {
string tag;
SDL_Rect rect;
SDL_Color color;
};壁を作るところは、ブロック等と同じ場所、setup_bricks関数の中にしておきます。前回のコードに付け足します。
std::vector<Brick> setup_bricks()
{
vector<Brick> bricks;
// setup paddle
...
// setup ball
...
// setup bricks
...
// setup walls
const int v_wall_width = 10;
const int v_wall_height = ScreenHeight;
const int h_wall_width = ScreenWidth - 2 * v_wall_width;
const int h_wall_height = v_wall_width;
const SDL_Color wall_color = {99, 38, 255, 255};
Brick left_wall = {
"wall",
{0, 0, v_wall_width, v_wall_height},
wall_color
};
Brick right_wall = {
"wall",
{ScreenWidth - v_wall_width, 0, v_wall_width, v_wall_height},
wall_color
};
Brick top_wall = {
"wall",
{v_wall_width, 0, h_wall_width, h_wall_height},
wall_color,
};
bricks.push_back(left_wall);
bricks.push_back(right_wall);
bricks.push_back(top_wall);
return bricks;
}やっていることは壁として扱う3つの画面左側面、画面天井、画面右側面にピッタリくっついたブロックの作成です。
コードは構造体の初期化をしているだけです。特に面白いところはありません。なにか言うところがあるとすると、ScreenWidth、ScreenHeightという定数ですが、これはグローバルな変数(定数)として定義しています。プログラムの冒頭で両方とも400としています。グローバルというのはだいたい関数の外側のことで、そこで定義された名前は、その翻訳単位、大雑把に言い換えるとC++のソースである.cppファイルのどこからでもアクセスできるようになります(ソースファイルをまたいでも非constのグローバル変数や関数名は外部リンケージを持つため同じ名前の定義が存在するとリンクエラーになります)。グローバル変数は、使い方にもよってその性質が違ってくるので一概には言えないのですが、少なくとも考えなしに何でもグローバルにするのは避けるほうが良いです。このプログラムでは画面サイズを取得しなければならないようなところが多いのですが、グローバルにしておかないと、この単純な設計では関数の引数として受け渡ししなければならず、関数の引数が多くなり見苦しくなってしまいます。constとしてあり、プログラムの他の場所では変更することが出来ない定数です。定数ならこの小さなプログラムの規模ではそれほど害があるとも思えないのであまり作り込まずグローバルとしておきます。
あともう一つ挙げるとすると、構造体の初期化について、構造体は初期化の時に{}の中に順番にその定義で宣言されたフィールドの順番通りに書いていくことでまとめて初期化することが出来ます。aggregate initializationと呼ばれます。この方法は一見便利そうですが、順番を正確に把握していないといけないのでかなり煩わしいし間違いをおかしやすいです。C++ではこの方法はそれほど使われません。代わりにコンストラクタを使った初期化の方が多く使われます。
実行すると以下のようになります。
壁が追加されました。色が微妙ですが…今は気にしないでおきます。ブロックの数が多すぎるのと小さすぎるのであとで直します。
ボールを動かす
ボールを動かすのにまず考えないといけないのが、最初にどの向きに進んでいくようにするかです。最初の方向が真上だと、仮に壁やブロックに跳ね返るようになっているとすると、いつまでも上下の往復を繰り返すようなことになりかねません。次に思いつくのはちょうど斜め45度に飛ばすことです。これなら壁に当たったりブロックに当たったりして跳ね返るときの動きが予想しやすくなります。しかし完璧とは言えず、毎回同じ方向に飛んでいくのはつまらないです。ある程度ランダムにしたりプレイヤーの操作で変化を加えられるようにしたいところです。しかし、問題は一つずつ片付けたほうがいいので今回は右斜め上に飛んでいくことにします。
次に考えるのが、斜め上移動するにはどうすればいいのだろうかということです。すでにパドルのところで横水平にうごかすのはやっています。パドルを動かすのは次のようなコードでした。
brick.rect.x += move_scale * dx;ここでdxには左キーが押されたら-1、右キーが押されたら+1が入っているようにしていました。もしdxが-1なら適当な移動量を調整するmove_scaleという係数とかけて、その分量だけパドルの現在位置xに足すと、xの値は小さくなるので左に移動しているように見えます。逆にdxが+1なら、現在位置xの値は大きくなるので、右方向に移動しているように見えます。ポイントとなるのは、このdxというのはただ移動する方向だけを意味しているということです。方向キーを押したとき、更新するのはdxの向きだけです。移動する量には関与していません。移動する量を調整しているのはmove_scaleという値です。このmove_scaleは最終的に1フレームに移動するピクセル量という結果になって描画されます
しかし、果たしてこのように向きと移動量を分けて考えることに意味があるのかという疑問がわきます。パドルの場合、次のようにすることも出来ました。
if (左キーが押されている) {
dx -= move;
}
if (右キーが押されている) {
dx += move;
}
brick.rect.x += dx;本題とは関係ないですが、変数の名前dxのdの意味について考えると、この場合はのdはdifferenceを意味していることになります。先の移動方向と量を分けて考える場合のdxのdは、directionのような意味ととらえると自然です。
このやり方でもパドルを動かす分には問題なかったでしょう。もう少し踏み込んで考えてみるとこの方法はある前提基づいているということが分かります。というのは移動する向きが常に水平方向だということです。仮に今少し斜め上にも動くようにしたいとなったとするとどうなるかを考えてみます。分かりやすいように具体的な数値をいれます。移動量が10で右斜め上45度に移動したいとします。右方向に10移動して、次に上に10移動します。フレームごとにこの移動を続ければ右斜め45度の移動はできます。次に右斜め上30度を考えてみます。まず右に10移動します。次に上に\(10 \times{} \frac{\sqrt{3}}{2} = 8.66025403784...\)になります。これはピタゴラスの定理あるいは直角三角形の比から出てきます。したがって、右に10、上に8.66025403784...という移動を毎フレーム続ければ右斜め上30度の移動ができることになります。
もうちょっと掘り下げてみてみます。
斜めの移動量
まず気になるのは、右に10上に10移動したとき、結果として見える移動量はもはや10ではないということです。右上45度の場合を考えると、\(\sqrt{10^2 + 10^2} = 10\sqrt{2} = 14.1421356237...\)となります。これはおかしなことでしょうか?現実に置き換えると奇妙な感じになります。例えば、自分の歩く速さを秒速1メートルで一定としたとき、右方向に10メートル進むのに10秒かかります。そして、右斜め前45度に10秒歩いたら同じように10メートル進みますが、このとき右方向の位置はまだ10メートルに達していないはずです。前方向も同様で、前にまっすぐ10秒歩いたら前に10メートル進みます。右斜め前に10秒歩いてもやはり前方向の10メートルの位置には達していないはずです。三角形にして考えると分かりやすいです。向きが逆になってしまいましたが図を貼っておきます。
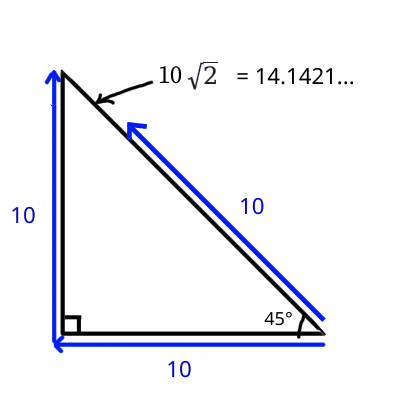
これが不自然に思えるのは、人間が歩くとき横方向の速さは秒速1メートルで、縦方向の速さは秒速1メートルなどと考えることはないからです。人間がある目的の位置に向かって歩くときは横だろうが縦だろうが斜めだろうが普通は前に向きを変えて前進します。カニ歩きをしたり後ろ向きで歩いたりしたため移動の速さが変わることはあるかもしれませんがそれはまた別問題です。ボールも同じです。ボールが右方向に秒速1メートル、上方向に秒速1メートルで飛んでいくとは日常的には考えません。
この現実の速さに対する人間の感覚は2Dゲームにおいてもそのまま当てはまるのか、という疑問がわきますが、当てはまる場合もあり、そうではない場合もあると思います。当てはまる場合としては、例えばビリヤードのゲームを作ったとしたとき、斜めに移動するとき移動量が大きくなるというのはいかにも不自然です。一方で、斜めに移動する場合も水平方向の速さと垂直方向の速さを維持したまま斜めの移動量が多くなる方が自然になる場合も多くあります。例えば古典的な2Dの縦スクロールシューティングゲームを考えると、右キーと上キーを同時に押したとき自機は画面右上に向かって進みます。右キーだけを押したときは右方向に進みます。もし、現実のように速さが同じなら移動距離も一定という考えを取り入れると、右上に進むときより、右方向に進むときのほうが移動速さが早く感じられるはずです。実際に作って操作してみると操作とシンクロしていなくて奇妙な感じを受けます。この辺りは必ずしも常に現実世界の法則を取り入れなくてもよく、ゲームにとって適した形にアレンジしていくことが必要になるかと思います。
正方形?
上で秒速という言葉が出てきましたが、現実の1秒あたりの移動するメートルといった1メートル/秒のようなものは速さとよばれます。今作ってるゲームでは1フレームあたりのピクセルの移動量がそれに対応していて、このままでは名前が長いし直感的でもないので、これから速さと呼ぶことにします。移動方向と速さを一つにまとめて扱うとき、必然的に水平方向の速さと垂直方向の速さの2つを扱うことになります。なぜかというと、速さひとつだけでは右上に進んでいるときと右下に進んでいるときの状態を区別できないからです。名前が長いので水平方向の速さをdx、垂直方向の速さをdyとします。今、スタート時に右斜め上に進んでいくことに決めました。このとき、速さが10とするとdx=10、dy=-10(SDLではy座標は数学の座標と違って画面下に向かって増えていくので上がマイナスです)となります。そして右の壁に当たったとき、dx=-10、dy=-10になります。
今度はどういうわけか真横右に移動するような事態になったとします。まず方向と速さを一緒にしている方ではdx=10、dy=0になります。これは何の計算も行っていなくて、単にyの速さを0にすればひたすら真横右に進むという点に着目しただけです。そして前の斜めの移動量のところで書いたとおり、右の移動量10を維持しています。さらに右斜め上30度と60度の場合はどうなるでしょうか。30度の場合は、dx=10、dy=\(-10 \times{} \frac{\sqrt{3}}{2} = 8.66025403784...\)になります。60度の場合はdx=\(10 \times{} \frac{\sqrt{3}}{2} = 8.66025403784...\)、dy=-10になります。ここから奇妙なパターンが見えてきます。
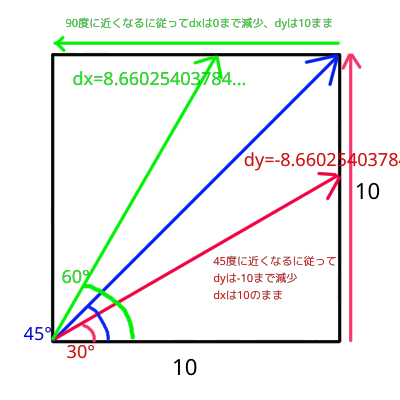
図から分かるのは、角度を少しずつ変化させるに従って、正方形の右辺、上辺をなぞるように水平と垂直の速さ(dxとdy)が変化していくということです。特に45度を堺に変化の仕方がガラリと変わります。
よくよく考えてみると2Dシューティングゲームでは8方向しか移動してない気がします。つまり右0、右上45、上90、左上135、左180、左下225、下270、右下315の45度刻みの8つです。経験から、2Dシューティングの場合、この方向に動くとき斜めの移動量は考慮しない方が自然な気がしています。もっと一般化すると、このように8方向への移動しか扱わない場合にだけそのような現象が起こるのではないかと思います。全くの推測ですが…もし360度全方位に移動することができる場合、うまく行くのか分かりません。もう一つやっかいなのは計算が面倒くさいということです。45度まではdx固定でdyを減少させ、45度から90度まではdxを減少させdyを固定と奇妙なパターンになります。
円で考える
今度は向きと速さを別に扱い、斜め方向の移動量を一定、つまり速さを一定とした場合を考えてみます。先の問題と合わせるために、右斜め上をdx=1、dy=-1としてそして速さを10としてみます。移動した分をax、ayとするとax=dx*10, ay=dy*10となります。そして右の壁に当たったとします。このときdx=-1、dy=-1となり、速さは10のままなのでax=-10、ay=-10となります。今は向きにxyとも1にしているのでたまたま前と一致しています。次に30度の右上を考えてみます。まず右斜め45度のとき、これを直角三角形と見ると斜辺の長さが\(\sqrt{10^2 + 10^2} = 10 \sqrt{2} = 14.1421356237...\)であることが分かります。斜辺\(10 \sqrt{2}\)に対し、直角三角形の比を使ってax=\(5 \sqrt{6}\)、ay=\(5 \sqrt{2}\)と求めることができます。
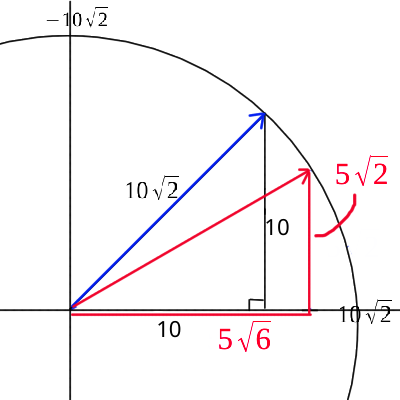
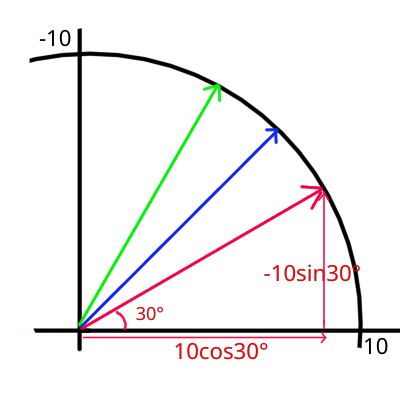
さっきは正方形の例に合わせるためにdx=1、dy=-1としましたが、これは使いづらいです。というのも、速さ10としたとき、移動する量がちょうど10にならないからです。dx、dyが作る三角形の斜辺の長さで割ることでこの調整が出来ます。dx=\(\frac{1}{\sqrt{2}}\)、dy=\(-\frac{1}{\sqrt{2}}\)とします。さらにもう一歩進めて三角関数を使うことであらゆる角度についての移動量を求めることができるようになります。例えば30°のときはax=10*cos30°、ay=-10*sin30°とすることが出来ます。
結局なんなのか
ここまで長々とどうでもいいようなことについて大して分かりやすくもない文章を書いてきたのは、ベクトルを導入しておきたいからです。ベクトルは数学の考え方ですが、ゲームやコンピューター・グラフィックスと相性がよくて頻繁に使われます。特に3Dグラフィックスでは必須のものです。数学と言ってもプログラミングにおいてはツールに近いです。さほど深い数学的な理解を持っていなくても、単純な計算ルールをいくつか覚えるだけで一応は便利に使えるようになります。しかし、ブロック崩しでどうベクトルを使うのかと言うと別に必須でもない気がします。長々と書いてきたやつの最後のケース、方向と速さをボールに持たせて、任意の角度に移動するような処理にはベクトルが使えます。
話をもとに戻して、今やりたいことは、ボールを右上に動かす、というそれだけです。
まずベクトルを構造体として定義します。
struct Vec2 {
double x;
double y;
};コードは極めて単純です。このxとyはベクトルの成分と呼ばれます。x成分とかy成分とか呼んだりします。ベクトルには多くの用途があり、フルに活用しようと思うと、たくさんコードを書かないといけないのですが、今回用意するのは二つです。
Vec2 normalized(const Vec2& v)
{
double length = sqrt(v.x * v.x + v.y * v.y);
return Vec2{v.x / length, v.y / length};
}これはベクトルの正規化と呼ばれる処理を行います。例えば方向ベクトルを適当に(1, -1)と取ったときその長さは\(\sqrt{2}\)になります。前に書いたように、長さが1でないと速さをかけたとき丁度いい移動量になりません。そこで、xとyの各成分をこの長さで割ってやることで、強制的に長さが1のベクトルに作り変えます。(1, -1)の場合、\((\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}})\)というベクトルが得られて、その長さは\(\sqrt{\frac{1}{\sqrt{2}}^2 + (- \frac{1}{\sqrt{2}})^2}\)で1になることが分かります。ベクトルの場合長さよりも大きさと呼ばれることも多いです。
他にもベクトル同士の足し算や掛け算のようなものがあるのですが今回は使いません。方向に速さをかけて移動量を計算するので、速さとの掛け算は必要になります。今使おうとしている速さはベクトルではありません。スカラーと呼ばれる何かの、ここではまさに速さの量を表すものなのですが、本質的にそれが何なのかは考えないことにします。ただ、ベクトルとスカラーの掛け算は決まってます。ベクトルをvとしてその成分をv.x、v.yとすると、スカラーsとの掛け算の結果はsv=(s*v.x, s*v.y)となります。関数にしておきます。
Vec2 scalar_multiplied(const Vec2 &v, double s)
{
return Vec2{v.x * s, v.y * s};
}名前が長すぎる気がしますが、今回は1箇所でしか使う予定がないので良しとします。ベクトルを使いこなして頻繁に使うようになったら考えることにします。
ボールの移動のコードを書く
ようやくここまで来ました。やろうとしていることは斜め上に動かす、ただそれだけです。
まずBrick構造体に向きのベクトルと速さのスカラーをもたせることにします。
struct Brick {
string tag;
SDL_Rect rect;
SDL_Color color;
Vec2 move_dir;
double move_scale;
};こうするとブロックや壁など動かないものまですべてが向きのベクトルと速さのスカラーを持つことになってしまい問題があります。しかし今は無視しておきます。無意味なデータを抱え込んでいてもそれを処理する側が無視してしまえば動作上は影響しません。まったく良い方法ではないので後で直すべき課題と記憶しておいて先に進みます。
追加したフィールドを初期化するコードをsetup_bricks関数に仕込みます。
vector<Brick> setup_bricks()
{
vector<Brick> bricks;
// setup paddle
...
// setup ball
Brick ball;
ball.tag = "ball";
ball.rect.w = paddle.rect.h * 1.2;
ball.rect.h = ball.rect.w; // square
ball.rect.x = paddle.rect.x + (paddle.rect.w / 2) - (ball.rect.w / 2);
ball.rect.y = paddle.rect.y - ball.rect.h;
ball.color = {255, 128, 200, 255};
ball.move_dir = normalized(Vec2{1.0, -1.0});
ball.move_scale = 3.0;
bricks.push_back(ball);
...
}右斜め上に3.0という謎の量だけ進むことを意図しています。
update関数でボールの位置を更新するようにします。
void update(vector<Brick>& bricks)
{
...
for (auto& brick : bricks) {
if (brick.tag == "paddle") {
brick.rect.x += move_scale * dx;
} else if (brick.tag == "ball") {
// ボールの位置を更新
Vec2 move = scalar_multiplied(brick.move_dir, brick.move_scale);
brick.rect.x += move.x;
brick.rect.y += move.y;
//~ ボールがパドルに当たったか判定
//~ ボールが壁に判定判定
//~ ボールがブロックにあたったか判定
} else if (brick.tag == "brick") {
//~ ボールが当たったブロックを消す
} else if (brick.tag == "wall") {
}
}
}実行してみます。
よく見るとちょうど右上45度ではなく上よりに進んでいます。この原因は浮動小数点数型であるdoubleと、整数型のintであるSDL_Rect構造体のxとyをごちゃまぜにして使っていることが原因です。どのように位置が変化しているかを確認するために、各フレームでのボールの位置を出力するコードをupdate関数に付け足します。
Vec2 move = scalar_multiplied(brick.move_dir, brick.move_scale);
brick.rect.x += move.x;
brick.rect.y += move.y;
SDL_Log("%d, %d", brick.rect.x, brick.rect.y);これを実行すると次のように出力されました。yが0になる付近に注目して途中部分だけを抜き出してあります。
INFO: 428, 17
INFO: 430, 14
INFO: 432, 11
INFO: 434, 8
INFO: 436, 5
INFO: 438, 2
INFO: 440, 0
INFO: 442, -2
INFO: 444, -4
INFO: 446, -6
INFO: 448, -8
INFO: 450, -10
INFO: 452, -12
INFO: 454, -14ボールは右と上に向かって動いていくので、xは増加してyは減少していきます。xは常に2ずつ変化していってますが、yは3ずつ変化していっています。そして0を堺に2ずつ変化するようになっている分かります。
たった1の違いではありますが、比率にすると2:3なので、1.5倍の違いが出てきてしまい大きな違いとなって現れます。問題を明らかにするために実験ようのコードを書いてみます。
doubleとintを混ぜて使う場合の実験
brick.rect.x += move.x と brick.rect.y += move.y というコードに問題があるのは確実なのですが、このコードはやや複雑なのでいくつかに分けてみていくことにします。
brick.rect.x(と.y)はSDL_Rect構造体のint型のフィールドです。move.x(と.y)はVec2のdouble型のフィールドです。演算子+=はa+=bとしたときa = a + bと同じ意味です。これをもっと単純な形にします。
int rx = 100; // 適当な値
double mx = 1.001; // 適当な値
rx = rx + mx; // intとdoubleを足した結果をintに代入
cout << rx << '\n';
//出力:
//1011.001と100を足した結果が101となりました。rxはintと宣言されていて、std::coutはオブジェクトの型によって適切な書式で出力してくれるので、出力される値の型はintとなり、101となるのは妥当に思えます。
もう一つ分けて考えられます。rx = rx + mx;という文には代入と足し算が混ざってます。rxはint型として宣言されているので、仮に右辺がdoubleの値100.001だった場合でもintに変換されて100になる、という推測はさほど違和感がないように思えます。しかし、=の右辺の rx + mx という式はどうなるのでしょう?intになるのかdoubleになるのか直感的な判断がしづらいです。これを実験してみます。
int rx = 100; // 適当な値
double mx = 1.001; // 適当な値
cout << rx + mx << '\n'; // intとdoubleのどっち?
//出力:
//101.001結果は小数点数として表示されました。std::coutが適切に型を判断してくれていることを考慮すると、intとdoubleを足した結果はdoubleになるのではないかと考えられます。これは暗黙の型変換と呼ばれるもので、算術演算子+-*/%についてはより情報が失われないように適切な型に変換されるようになっています。ちょっと分かりづらいですがここに書かれていました。他の参考資料としてはCクイックリファレンスという本の第4章にも書かれています。
Usual arithmetic conversions
The arguments of the following arithmetic operators undergo implicit conversions for the purpose of obtaining the common real type, which is the type in which the calculation is performed:
以下の算術演算子の引数は、計算が実行された型の中で共通の実数型を結果として得る目的のために、暗黙の型変換が行われる。
- binary arithmetic *, /, %, +, -
- relational operators <, >, <=, >=, ==, !=
- binary bitwise arithmetic &, ^, |,
- the conditional operator ?:
1) If one operand is long double, long double complex, or long double imaginary, the other operand is implicitly converted as follows:
もしオペランドの一つがlong double、long double complex、long double imaginaryならば、もう一つのオペランドは以下に従って暗黙的に変換される:
- integer or real floating type to long double
整数もしくは実数の浮動小数点数の型はlong doubleに変換される
- complex type to long double complex
- imaginary type to long double imaginary
2) Otherwise, if one operand is double, double complex, or double imaginary, the other operand is implicitly converted as follows:
そうではなく、もしオペランドの一つがdouble、double complex、double imaginaryならば、もう一つのオペランドは以下に従って暗黙的に変換される:
- integer or real floating type to double
整数もしくは実数の浮動小数点数の型はdoubleに変換される
- complex type to double complex
- imaginary type to double imaginary
以下省略...
Implicit conversions (Usual arithmetic conversions) - cppreference.com
このようなルールがあるため、rx + mx という式はdoubleに変換されることになり、実験の結果とも一致します。一方で、rx = mx については、rxがintとはっきり宣言されているので、情報を失ってでもrxの型であるintに変換されます。合わせて考えるとrx = rx + mx;という文では、まず+で1回、=で1回、int+double→double→int、と暗黙の型変換が2回行われていることとなります。
変換のルールが分かったので次に加算する値がプラスとマイナスのときでどのように影響するかをみてみます。
int rx = 100; // 適当な値
int ry = 100; // 適当な値
double mx = 1.001; // 適当なプラスの値
double my = -1.001; // 適当なマイナスの値
cout << rx + mx << ',' << rx + my << '\n';
rx = rx + mx;
ry = ry + my;
cout << rx << ',' << ry << '\n';
cout << "---------\n";
// intの方をマイナスにしてみる
rx = -100;
ry = -100;
cout << rx + mx << ',' << rx + my << '\n';
rx = rx + mx;
ry = ry + my;
cout << rx << ',' << ry << '\n';
//出力:
//101.001,98.999
//101,98
//---------
//-98.999,-101.001
//-98,-101出力が見にくいので表にしておきます。
| intの値 r | doubleの値 m | r + m (int+double) | r = r + m (int=int+double) | 増分 |
|---|---|---|---|---|
| 100 | 1.001 | 101.001 | 101 | +1 |
| 100 | -1.001 | 98.999 | 98 | -2 |
| -100 | 1.001 | -98.999 | -98 | +2 |
| -100 | -1.001 | -101.001 | -101 | -1 |
101.001→101と98.999→98となっているところに注目すると、前者は102よりも101というより近い方の整数に変換されていますが、後者は99よりも98というより遠い方の整数に変換されています。
もう一つの-98.999→-98と-101.001→-101となっているところに注目すると、前者は-99よりも-98というより遠い方の負の整数に変換されていて、後者は-102よりも-101というより近い方の整数に変換されています。
どのようにdoubleがintに変換されるのかに注目すると、どちらの整数に近いとかは全く考慮されずに、単純に小数点以下が捨てられて、整数部だけをintの値として使っていることが分かります。果たして、この暗黙のdoubleからintへの変換において、小数点以下が問答無用で切り捨てられるという動作は常にそうであると期待していいのでしょうか?例によってcppreference.comから該当する記述を探すと、次のように書かれているのを見つけました。
Floating–integral conversions
A prvalue of floating-point type can be converted to a prvalue of any integer type. The fractional part is truncated, that is, the fractional part is discarded. If the value cannot fit into the destination type, the behavior is undefined (even when the destination type is unsigned, modulo arithmetic does not apply). If the destination type is bool, this is a boolean conversion (see below).
浮動小数点数型のpvalueは整数型のpvalueの変換できる。小数部は切り捨てられる、すなわち、小数部は破棄される。もし値が変換先の型に収まらなければ、動作は未定義 (たとえ変換先の型が符号なしであっても、剰余演算は適用されない)。もし変換先がboolであれば、ブーリアンの変換となる (下を参照)。
A prvalue of integer or unscoped enumeration type can be converted to a prvalue of any floating-point type. If the value cannot be represented correctly, it is implementation defined whether the closest higher or the closest lower representable value will be selected, although if IEEE arithmetic is supported, rounding defaults to nearest. If the value cannot fit into the destination type, the behavior is undefined. If the source type is bool, the value false is converted to zero, and the value true is converted to one.
Implicit conversions (Floating–integral conversions) - cppreference.com
どうも小数点以下が常に切り捨てられると考えて良さそうです。
C++の振る舞いは分かりましたが、問題は解決していません。同じ量だけdoubleを足しても+方向と-方向でボールの移動量が変わってきてしまうのでは困ります。問題の根本的な原因はdoubleとintをごちゃまぜに使っていることです。浮動小数点数はデリケートで難しい領域なので、もし整数だけを使ってことを済ませられるならできればそうしたいところです。しかし、ここまでやってしまったので今さら後戻りしたくないというやや不純な動機から、ベクトルはdoubleとしておきたいです。今分かったように、何も考えずにdoubleとintの変換を行うと問題が発生する可能性が高いです。対策を少し考えてみます。
今回の場合、対策は簡単です。表の101.001→101と98.999→98のところで、増分がそれぞれ+1と-1になるように、doubleからintへの変換を101.001→101と98.999→99となるように調整すればいいわけです。要は四捨五入すればいいわけです。四捨五入するには演算結果が正の場合は+0.5、負の場合は-0.5してから通常の型変換を適用するということも考えられますが、C++の標準ライブラリに用意されているstd::roundという関数を使います。
前の実験用コードでstd::round関数を使ってみます。
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
int rx = 100; // 適当な値
int ry = 100; // 適当な値
double mx = 1.001; // 適当なプラスの値
double my = -1.001; // 適当なマイナスの値
cout << rx + mx << ',' << rx + my << '\n';
rx = round(rx + mx);
ry = round(ry + my);
cout << rx << ',' << ry << '\n';
cout << "---------\n";
// intの方をマイナスにしてみる
rx = -100;
ry = -100;
cout << rx + mx << ',' << rx + my << '\n';
rx = round(rx + mx);
ry = round(ry + my);
cout << rx << ',' << ry << '\n';
}
//出力:
//101.001,98.999
//101,99
//---------
//-98.999,-101.001
//-99,-101もう一度表にしておきます。
| intの値 r | doubleの値 m | r + m (int+double) | r = round(r + m) (int=round(int+double)) |
増分 |
|---|---|---|---|---|
| 100 | 1.001 | 101.001 | 101 | +1 |
| 100 | -1.001 | 98.999 | 99 | -1 |
| -100 | 1.001 | -98.999 | -99 | +1 |
| -100 | -1.001 | -101.001 | -101 | -1 |
これが欲しかったものです!
ボールの移動にstd::round関数を使う
さっそくボールの移動のところを修正します。update関数の中です。
void update(vector<Brick>& bricks)
{
...
for (auto& brick : bricks) {
if (brick.tag == "paddle") {
brick.rect.x += move_scale * dx;
} else if (brick.tag == "ball") {
Vec2 move = scalar_multiplied(brick.move_dir, brick.move_scale);
brick.rect.x = round(brick.rect.x + move.x);
brick.rect.y = round(brick.rect.y + move.y);
SDL_Log("%d, %d", brick.rect.x, brick.rect.y);
} else if (brick.tag == "brick") {
} else if (brick.tag == "wall") {
}
}
}実行してみます。
意図したとおり右斜め上45度に進んでいます。
念の為位置をコンソールに出力したものを確認しておきます。
INFO: 552, 10
INFO: 554, 8
INFO: 556, 6
INFO: 558, 4
INFO: 560, 2
INFO: 562, 0
INFO: 564, -2
INFO: 566, -4
INFO: 568, -6
INFO: 570, -8
INFO: 572, -10
INFO: 574, -12xとy両方ともちゃんと2ずつ変化しています。
次に続く
ボールが跳ね返ってブロックに当たったら消えるところまで書くつもりでしたがあまりに長くなりすぎたのでここで一旦切っておきます。