pcat (6) 地面に立つ
前回は猫と地面、もとい丸と四角を描くだけというおそろしくつまらない内容でした。今回は丸と四角で衝突処理をして、丸が四角の上に乗っかるようにします。またつまらない回になりそうな予感がしないでもないです。
やることは以下のとおりです。
- 猫は初期位置から下に落ちてくるようにする。
- 猫は地面の上に接したらそれ以上落ちないようにする。
- 猫はキーボードの左右キーで左右に動けるようにする。
- 猫は下に地面がない場所に移動したら下に落ちるようにする。
コードは前回の終了時点のものをそのまま引き継いで使って、付け足していくようにします。
自由落下
イタリアの学者ガリレオ・ガリレイは、重いものほど早く落下するという当時の説が馬鹿げていると考えて、ピサの斜塔から重さの違う2つのものを落としてその間違いを明らかにしようとしたという逸話があります。現代の初歩的な物理の知識によれば、物体を空から落としたとき、空気抵抗がないものとすると、落下速度v、重力加速度g、経過時間tとすると\(v = gt\)となるそうです。この式は落下速度は時間にのみ比例して大きくなるのであって、重さは全く関係ないことも表しています。重力加速度gは、地球表面上では\(9.80665m/s^2\)だそうです。したがって、適当な高さからものを落とした場合、1秒後のvは9.80665m/sとなります。
さて、今ゲームの初期状態では猫は空中に配置されます。ゲームが開始した瞬間そこから落ちていくようにします。比較のために、一旦先の\(v=gt\)の法則を無視します。常に一定の速度で落下する場合、例えば、1秒間に100ピクセル落ちるとすると\(v=100\)となるでしょう。これをコードにするのはとても簡単です。
void Cat::update(float dt) {
position_.y += 100.0 * dt; // 1秒間に100.0ピクセル下に落ちる
// CircleShape型のメンバ変数も位置を持つので合わせて更新しておく
shape_.setPosition(position_.x, position_.y);
}ついでに猫の初期位置は画面一番上にしておきます。
void setup() {
g_cat = new Cat{{ScreenWidth / 2.0, 0}}; // Catの初期位置はおおよそ水平中央の一番上にする
...
}実行すると次の画面のようになります。
いまいちな感じがします。なので現実の落下速度の法則\(v=gt\)を適用してみることにします。
ここでgの値をどうするかですが、今のゲームではメートル単位を使っていないし今後も使う予定もありません。したがって9.80665という値は意味をなしません。まず\(g=1\text{dot}/s^2\)で始めてからちょうどよくなるように調整していくことにします。
ここで問題なのが経過時間tをどのように取るかです。一つの方法はCatにメンバ変数としてtをもたせて、落下を開始した瞬間からフレームの更新ごとにtを累積していく方法です。これでもおそらく機能するでしょうが落下が始まるたびにtをリセットしたり加算したり管理が面倒です。もう一つの方法は経過時間を直接扱うのではなく、現フレームの落下速度を前フレームから算出する方法です。\(v=gt\)を使ってちょっとした細工をします。前フレームをt1とすると\(v_{t_1}=g{t_1}\)、現フレームをt2とすると\(v_{t_2}=g{t_2}\)と描くことが出来ます。現フレームと前フレームの差を取ると、\(v_{t_2} - v_{t_1} = g(t_2 - t_1)\)となり、これを整理して\(v_{t_2} = v_{t_1} + g(t_2 - t_1)\)となります。前フレームからの経過時間\(t_2-t_1\)はupdate関数の引数dtによって得られます。こちらの方法を取る場合は、前フレームの落下速度をメンバ変数として持たせる必要があります。どちらを採用するかですが、2つ目の方にします。メンバ変数が表しているものが「落下が始まってから経過した時間」という変数よりも、「直前のフレームでの落下速度」という変数の方が直感的に思えるからです。
この落下速度を適用するのも難しくありません。
const float Gravity = 9.8; // グローバル定数
class Cat : public sf::Drawable {
...
private:
sf::Vector2f position_;
sf::CircleShape shape_;
float vertical_velocity_; // 追加 落下速度 コンストラクタで0に初期化すること
};
void Cat::update(float dt) {
vertical_velocity_ += Gravity * dt; // 落下速度を更新 v2 = v1 + g(t2 - t1)
position_.y += vertical_velocity_; // 落下させる
shape_.setPosition(position_.x, position_.y); // CircleShapeも合わせて更新
}Gravityの値はいくつか試しましたが、結局9.8付近がちょうど良さそうでした。これを実行すると次のようになります。
まずまずな感じなのでこれを採用します。
地面の上に立つようにする
地面の上に立つとは、もう少し噛み砕くと、ちょうど地面の上に猫が接するような位置で止まるようにすることです。まず明らかに必要なことは、地面と猫がぶつかったことを検出する仕組みです。まずはそれだけを考えてみます。
今は猫は上から落ちてくるだけであるので、ぶつかったとき猫は必ず上方向から地面に入ってきたことになります。それ以外のケースは考えないようにします。
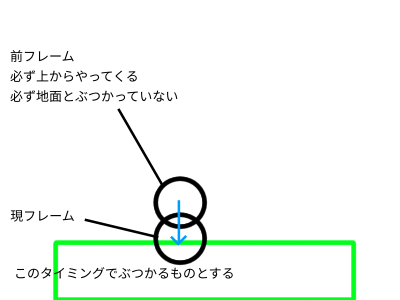
まずはここまで作ってしまいます。試験的にぶつかったことを通知するために、グローバルなフラグを使います。フラグがセットされているときは、updateでこれ以上落ちないようにしておきます。そうすることでぶつかったことを視覚的に確認することが出来ます。
bool g_intersected = false; // グローバルなフラグ
void Cat::update(float dt) {
if (g_intersected) return; // もし一度でも交差したらそれ以降は何もしない
vertical_velocity_ += Gravity * dt;
position_.y += vertical_velocity_;
shape_.setPosition(position_.x, position_.y);
if g_cat と g_ground が 交差していたら then // 交差判定を行う処理が必要
g_intersected = true;
}今作らないといけないのはコメントにあるようにCatとGroundの交差判定を行う処理です。Catは一つの円、Groundは複数の長方形から出来ています。やることは、一つの円に対し、順番に複数の長方形と交差判定を行っていくことです。ここでまず問題になるのが、円と長方形の交差判定です。円同士や長方形同士の交差判定はさほど難しくないのですが、円と長方形の判定はやや複雑になります。猫を丸にしたことを少し後悔しています。
自力で考えてもいい方法が思いつかなかったのでStack Overflowのこの投稿を検討してみました。Web上のソースコードを利用するときに注意しておきたいのがライセンスです。Stack Overflowの投稿に適用されるライセンスについてはこちらやこちらに書かれています。先の投稿の場合CC BY-SA 2.5ということになります。Creative Commonsはかなり「ゆるい」といったらなんですが使いやすいライセンスです。なので先の投稿のコードを使っても良かったのですが、今回の場合、円と長方形の判定はさして大きな関心ごとではなく、円を長方形とみなして、長方形同士の判定にしても支障はないでしょう。という言い訳をして、猫は丸の見た目をしているにも関わらず、当たり判定があるのはその円に外接する正方形とすることにします。
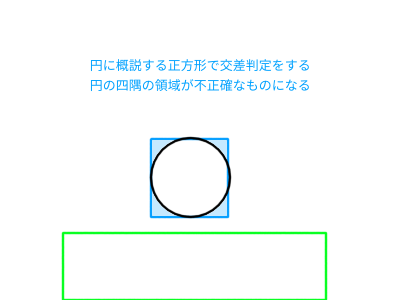
長方形同士の交差判定は比較的難しくない、というよりSFMLに用意されているのでそれを使います。sf::Rect<T>のメンバ関数intersectsです。intersects関数を利用するためには、sf::Rect<T>が必要になります。これはsf::Shapeを継承するsf::CircleShapeとsf::RectangleShapeのメンバ関数getGlobalBoundsで取得することが出来ます。この2つを使って交差判定を書きます。
void Cat::update(float dt) {
if (g_intersected) return; // 一度でも交差したらもう何もしない
// 落下速度を更新して位置も更新
vertical_velocity_ += Gravity * dt;
position_.y += vertical_velocity_;
shape_.setPosition(position_.x, position_.y);
// 地面のそれぞれのブロックと交差判定を行う
auto cat_rect = shape_.getGlobalBounds();
for (int i = 0; i < g_ground->count(); ++i) {
auto ground_rect = g_ground->shape(i).getGlobalBounds();
if (ground_rect.intersects(cat_rect)) {
// 交差した
g_intersected = true; // フラグをセット
break; // これ以上調べる必要はない
}
}
}
// 保持する地面のブロックにアクセスできるようにメンバ関数を2つ追加
class Ground : public sf::Drawable {
public:
...
// 地面のブロックの数 ループで走査するために必要
int count() const { return blocks_.size(); }
// 保持するRectangleShapeをインデックスで指定して取得
const sf::Shape &shape(int i) const { return blocks_.at(i); }
...
};実行すると次のようになります。
背景が青だと黒丸が見にくいので白にしました。
上の場合はあまり明らかではないけど、落下速度の設定によっては地面にめり込んでしまいます。試しにconst float Gravity = 29.8;として、Gravityを9.8から29.8に変更してみます。
今度ははっきりと地面にめり込んでいるのが確認できます。期待するのは地面にめり込まずにちょうど接する位置で止まることです。次はこれを修正することにします。
あるフレームのCat::updateにおいて、ちょうど交差していると判定されるとします。このとき、交差していると判定される以上、猫と地面は接しているのではなく、少なくとも1ピクセル以上は重なっている、つまりめり込んでいることになります。別の言い方をすると、ちょうど接しているフレームというのは交差判定からは検出できないことになります。したがって、地面に接する位置で止まるようにするために取れる手段は、いったん交差していることを検出してから、ぎりぎり交差しない位置まで猫を押し戻すことです。
問題となるのが、どれだけ押し戻せばいいかです。いくつか方法が考えられますが最も単純なのは次のようなものです。
- 上から落ちてくることはわかりきっているので、押し戻す方向は上方向である。
- ①猫を1ピクセル上に移動させてみる。
- ②ぶつかった地面のブロックと交差判定を行う。
- まだ交差していれば、交差しなくなるまで①②を繰り返す。
- 交差しなかったときがちょうど接する位置なので、このフレームの位置として更新する。
これをコードにしてみます。
void Cat::update(float dt) {
if (g_intersected) return;
vertical_velocity_ += Gravity * dt;
position_.y += vertical_velocity_;
shape_.setPosition(position_.x, position_.y);
// CircleShapeのGlobalBoundsは円の外1ピクセルを必要とするので、そのまま使うと1ピクセルずれてしまう
// GlobalBoundsをそのまま使うことが出来ないので、円の上下左右を通過する矩形を手動で求める
// auto cat_rect = shape_.getGlobalBounds(); // これは使えない
sf::FloatRect cat_rect{position_.x, position_.y, 2 * shape_.getRadius(),
2 * shape_.getRadius()};
for (int i = 0; i < g_ground->count(); ++i) {
// RectangleShapeのGlobalBoundsは引き続き使用可能
auto ground_rect = g_ground->shape(i).getGlobalBounds();
if (ground_rect.intersects(cat_rect)) {
// 1ピクセルずつ上にずらしながら、ちょうど交差しなくなる位置、つまり接する位置を求める
do {
cat_rect.top -= 1;
} while (ground_rect.intersects(cat_rect));
// 上で求めた位置をこのフレームの位置として使う
position_.y = cat_rect.top;
shape_.setPosition(position_.x, position_.y);
g_intersected = true; // フラグ更新
break; // これ以上検索しない
}
}
}実行すると、ちょうど地面の上に丸が触れるところで止まっているようになります。
一見うまく行っているように見えるですが、微妙なバグを含んでいます。それはSFMLのShape(を継承するCircleShapeやRectangleShapeを含む)のdraw関数の浮動小数点数の扱いが原因です。drawの動作をいくつか試して確認してみたところ、どうもfloatとして保持するpositionを実際に描画するときにはround(四捨五入)した位置に描画するようです。
具体的にどのようになるかというと、CircleShapeのc1とc2があるとします。c1のposition.yが100.4でc2のposition.yが100.5だとします。そうすると、c1はピクセル座標100に、c2はピクセル座標101に描画され、1ピクセルのずれが生じます。この挙動が望ましいかどうかは場合によります。今回の場合は、そのような動作は期待していませんでした。
どのような結果になるかを、先のコードを書き換えて見てみます。変更点は以下のとおりです。
- ぶつかったら更新をストップすることで、ごまかしていたのをやめる。
- 地面と交差していたら落下速度を0にリセットする。
- Cat::draw関数で、shape_変数のコピーを作成して、切り捨て(truc)と四捨五入(round)で違いを確認できるようにする。
これを取り込んだコードは次のようになります。
void Cat::update(float dt) {
// if (g_intersected) return; // 削除 フラグに関係なく処理を続ける
// 地面に着地しても落下を適用する
vertical_velocity_ += Gravity * dt;
position_.y += vertical_velocity_;
shape_.setPosition(position_.x, position_.y);
sf::FloatRect cat_rect{position_.x, position_.y, 2 * shape_.getRadius(),
2 * shape_.getRadius()};
for (int i = 0; i < g_ground->count(); ++i) {
auto ground_rect = g_ground->shape(i).getGlobalBounds();
if (ground_rect.intersects(cat_rect)) {
// g_intersected = true; // 削除 もうフラグは必要ない
// 地面にちょうど接する位置に調整
do {
cat_rect.top -= 1;
} while (ground_rect.intersects(cat_rect));
position_.y = cat_rect.top;
shape_.setPosition(position_.x, position_.y);
vertical_velocity_ = 0; // 落下速度を0にリセットする
break;
}
}
}
void Cat::draw(sf::RenderTarget &target, sf::RenderStates states) const {
// 切り捨て(trunc)を適用したCircleShape
auto s1 = shape_; // コピー
s1.setPosition(40, std::trunc(shape_.getPosition().y)); // yだけ変更
// 四捨五入(round)を適用したCircleShape
auto s2 = shape_; // コピー
s2.setPosition(100, std::round(shape_.getPosition().y)); // yだけ変更
target.draw(s1); // ①trunc
target.draw(s2); // ②round
target.draw(shape_); // ③元のまま
}実行すると、3つのCircleShapeが描画されます。
左の円から順に上記コードのコメントにある①②③です。よく見ると②と③は下まで行ったらガクガク震えているのがわかります。①は安定しています。
さらによく目を凝らしてみると、①の下に1ピクセルの隙間があることがわかります。これは交差判定の処理が原因のバグです。sf::Rect<float>、つまりsf::FloatRectのintersects関数は、矩形の保持する情報の型であるfloatを使って交差判定を行います。そのため、例えば地面のトップが10.0、猫のボトムが10.1となったとき、これは交差すると判定されます。そして猫を1ピクセル上に移動させるので、猫のボトムは9.1となります。これをdrawのとき切り捨てて描画するので1ピクセルの隙間が出来ます。これも合わせて修正するには猫の当たり判定を行う矩形の座標も切り捨て(trunc)してしまう必要があります。
void Cat::update(float dt) {
...
// 判定に使う矩形のy位置は、切り捨てる
sf::FloatRect cat_rect{position_.x, std::trunc(position_.y),
2 * shape_.getRadius(), 2 * shape_.getRadius()};
...
}
void Cat::draw(sf::RenderTarget &target, sf::RenderStates states) const {
// yは四捨五入ではなく切り捨てたもの使う
auto s = shape_; // コピーが必要
s.setPosition(40, std::trunc(shape_.getPosition().y));
target.draw(s);
}こうすることで①で見られた1ピクセルの隙間もなくなり、期待する結果が得られます。
しかし、これらは応急処置に過ぎず、根本的な解決策ではありません。今解決策を追求していくと、本題から逸れてしまうので一旦これで進めてみます。
地面の上を歩く、そして落ちる
次のステップは、着地後に左右に歩けるようにすることです。まずキーを受け付けなければいけません。SFMLでキーボード入力を検出するには2つの方法があります。
- ウィンドウのイベントから取得する方法。
- sf::KeyboardのisKeyPressed関数を使う方法。
イベントで取得するにはmain関数のメインループのイベントを処理しているところに処理を追加します。
// main関数の一部
...
while (window.isOpen()) {
sf::Event event;
while (window.pollEvent(event)) {
if (event.type == sf::Event::Closed) {
window.close();
} else if (event.type == sf::Event::KeyPressed) {
switch (event.key.code) {
case sf::Keyboard::Escape:
case sf::Keyboard::Return:
window.close();
break;
case sf::Keyboard::Space:
paused = !paused;
clock.restart();
break;
case sf::Keyboard::Left: // 追加 左キーが押された
g_cat->move(-1); // 猫を左へ移動
break;
case sf::Keyboard::Right: // 追加 右キーが押された
g_cat->move(+1); // 猫を右へ移動
break;
default:
break;
}
}
}
...
}
...イベントでは、キーを押しっぱなしにしたときなど、正確に毎フレームの入力を取得することが出来ません。イベントではゲームプレイの操作感に影響するような厳密な入力の処理を必要とするものを扱うべきではないでしょう。isKeyPressed関数を使えば、正確にキーの状態を取得することが出来ます。今回は手抜きしてイベントの方で処理します。isKeyPressedを使う方法はこちらのチュートリアルが参考になるかと思います。
上のコードではCat::moveという関数で猫を左右に移動させています。この関数はまだ用意していないので追加します。
class Cat : public sf::Drawable {
public:
...
void move(float dx);
...
};
void Cat::move(float dx) {
const float speed = 10.0; // 適当な移動量
position_.x += speed * dx;
shape_.setPosition(position_.x, position_.y);
}実行すると次のようになります。
左右に動けるようになって、地面のないところでは再び落ちていくようになりました。
次やることはジャンプできるようにすることです。しかし、だいぶ長くなってきたので一旦ここで切ります。