Lua入門その4 — 数値と計算と条件分岐

1 何をするか

練習のために前回よりもう少し複雑な計算をやります。基本的な作りは前回と同じです。ただし、新たに条件分岐を使う必要があります。

2 問題4

今回の問題は次の通りです。

問題4 — 二次方程式の解

次のような二次方程式を考える。

\(ax^2 + bx + c = 0\)

コマンドライン引数で、前から順番にa、b、cと3つの係数の値を引数として受け取る。その方程式について、\(x\)の実数解を求める。

二次方程式の解は、次の式で求まるものとする。

\(\large x = \frac{-b \pm \sqrt{b^2 -4ac}}{2a}\)

求めた値を画面に表示する。

解が2つの場合は x = 1, 2 のように表示する。
重解の場合は x = 1 のように表示する。
実数解を持たない場合は no real solution と表示する。

BMIの計算よりは複雑です。しかし、考え方はほぼ一緒です。

数学の話をしたい訳ではないので、なぜ上の式で解が求まるのか書かないでおきます。気になる場合は、「二次方程式解証明」などでググると出てくるかと思います。ちょっとした変形を施すだけで、そんなに難しくないです。

今回新たに覚えなければいけないのは、結果の表示の仕方を場合に応じて分けなければいけないことです。 Luaには、if文というものがあります。 if文を使えば条件によって処理を分岐させることができます。今回の目玉はこのif文となるでしょう。

もう一つ新たに登場するのは、平方根を求める方法です。これは、標準ライブラリと呼ばれる道具箱のようなものの中に用意されています。その道具箱から適したものを見つけて利用します。

2.1 二次方程式とは

二次方程式とは、問題にあるような \(ax^2 + bx + c = 0\) という形をした方程式です。ここで、xが未知の値です。そして、二次方程式を解くということは、この方程式を満たす未知のxの値を求めることです。 a、b、cは既知の値です。つまり a = 1、b = 2、c = 3 とかいった具体的な値が入っていると想定しておきます。仮に、a = 1、b = 2、c = -8 としてみます。このとき、元の方程式に代入すると \(x^2 + 2x - 8 = 0\) となります。因数分解をしてやると \((x - 2)(x + 4) = 0\) になります。この方程式を満たすxの値、つまり、左辺が0となるxの値は2つあり、2と-4です。実際に x = 2、または、x = -4 を代入してみると、どちらも左辺が0となることが分かるでしょう。

二次方程式の解を視覚的に理解することもできます。さっき使った方程式を \(y = x^2 + 2x - 8\) と二次関数に置き換えてやります。そして、この関数を直交座標系のXY平面上にプロットしてやります。

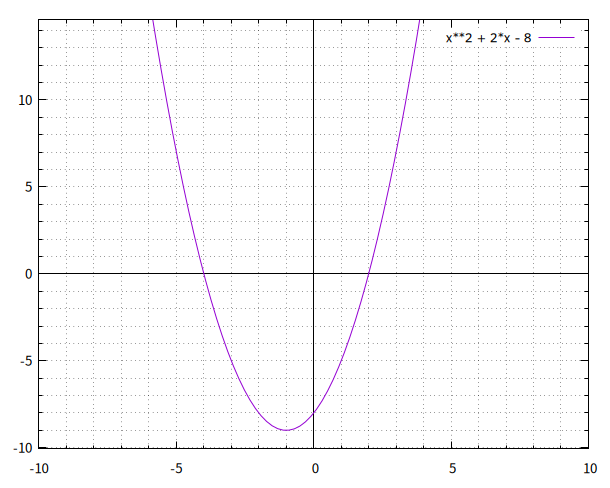
quadratic function plot 1

図1: \(y = x^2 + 2x - 8\) のグラフ

縦がyで横がxであり、縦のx=0のところの線がy軸で、横のy=0のところの線がx軸であると考えて下さい。そして、yが0であるところ、つまり、プロットした放物線がx軸と交わるところに注目します。 yが0であるということは、\(0 = x^2 + 2x - 8\) であり、これは左辺と右辺を逆にすれば、元の方程式と同じです。このことから、yが0となるときのxの値である、x軸と放物線が交わるx座標の値が、元の二次方程式の解ということになります。

これだけで終われば楽なのですが、二次方程式にはちょっと厄介な(面白い？)ところがあります。

a、b、cの値をそれぞれ1、4、4とします。こうしたときに得られる二次関数 \(y = x^2 + 4x + 4\) をプロットすると次のようになります。

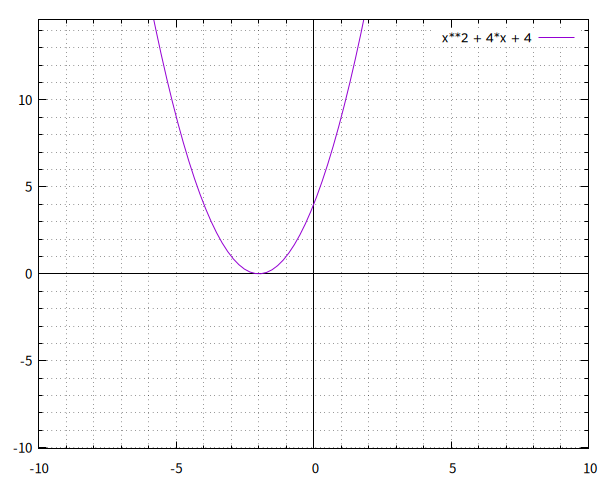
quadratic function plot 2

図2: \(y = x^2 + 4x + 4\) のグラフ

放物線とx軸との交差するところが、曲線のちょうど底(頂点と呼びます)になっています。このとき交差する点は一つしかありません。言い換えるとx軸と接している状態です。また元の二次方程式の解も一種類で、-2です。一種類といって、一つと言わなかったのは、解が一つしかないのではなく、重なっていると考えるからです。呼び名がついていて重解を持つと言います。

さらに放物線を上方向にスライドさせるために、a、b、cの値をそれぞれ1、4、6としてみます。こうしたときに得られる二次関数 \(y = x^2 + 4x + 6\) をプロットすると次のようになります。

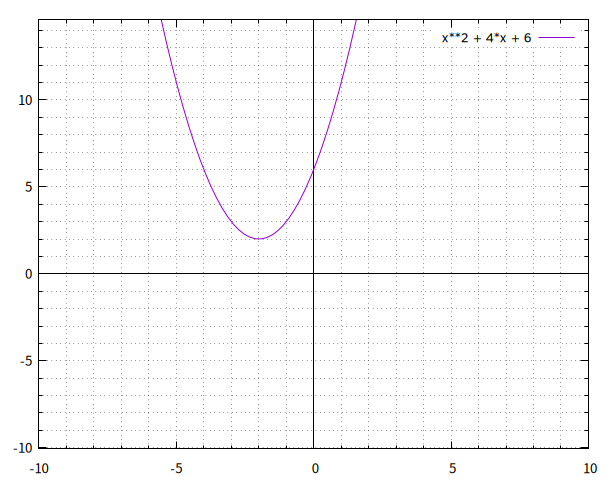
quadratic function plot 3

図3: \(y = x^2 + 4x + 6\) のグラフ

見てすぐ分かるとおり、x軸と交わることも接することもありません。このような場合は、元の二次方程式は実数解を持ちません。実数といったところが微妙なところで、実数ではない解 虚数解 なら持つとみなせます。そのためには、数の領域を実数の世界から飛び出して、複素数まで拡張しなければなりません。今回の問題では、複素数は扱わずに、単に「no real solution (実数解なし)」とだけ表示させるとしておきました。

これ以上やると詳しくなりすぎて危険人物扱いされかねないので、ここら辺にしておきます。

2.2 問題の吟味

二次方程式には興味深い所がありますが、今回やるのは前回BMIの計算でやったのと同じように、あらかじめ決められた計算を行うだけです。そのために必要なことを洗い出してみます。

コマンドラインから3つの引数を受け取る。
コマンドラインから受け取った引数は文字列なので、数値に変換する。
あらかじめ決められた計算式 \(\large x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) のa、b、cに3つの引数から得た数値を入れて計算する。
- 平方根の根の部分 \(b^2 - 4ac\) 計算して、正の場合、0の場合、負の場合で分岐する。
  - 正の場合、解を2つ求めて、表示する。
  - 0の場合、解を1つ求めて、表示する。
  - 負の場合、「no real solution」と表示する。
平方根の計算をする方法をが必要。

加えて、前回のBMIでやった変数は今回も利用する必要があります。というより、変数は今後作成するほとんどのプログラムで必要となるので、いちいち書かないでおきます。

これらをやっていけば、おそらく問題の解答に辿りつくでしょう

2.3 作業場所を確保する

これまでと同じように、ディレクトリを作成して作業場所を確保します。

% cd ~/code/pintro⏎ ▹このシリーズ用のディレクトリに移動 ~/code/pintro は前回までで作成済とする
% mkdir problem4⏎   ▹この問題用のディレクトリを作成
% cd problem4⏎      ▹作成したディレクトリの中に移動
% pwd⏎              ▹カレントディレクトリのパスを表示
/home/toma/code/pintro/problem4

ユーザー名tomaは、自分の利用しているユーザー名に置き換えてください。

これで作業場所は用意できました。

2.4 if文

今回の問題では、二次方程式の係数に応じて、結果が3つのケースに別れることになります。これまで紹介したLuaの機能だけでは、目的を達成することは難しいです。先に 条件分岐 を可能とするLuaの機能を紹介しておきます。

条件分岐とは、条件によって処理を振り分けることです。例えば、ある変数aがあったとして、この変数の値が1のときは「ONE」と表示させる、といった感じです。これをLuaで書くと、次のようになります。

if a == 1 then print "ONE" end

ifとthenの間に書かれているのが条件です。条件が真とみなせる値のときに、thenからendまでのものが実行されます。試しに対話モードでやってみましょう。

> a = 1⏎                          ▹変数aの値を1にセットする
> if a == 1 then print "ONE" end⏎
ONE
> a = 2⏎                          ▹変数aの値を2にセットする
> if a == 1 then print "ONE" end⏎
>                                  ▹何も表示されなかった

条件の a == 1 は、「aが1と等しいなら真」という結果を返す式です。イコール「=」を二つ繋げることに注意してください。一つだけだとそれは代入を意味することになってしまい、条件には使えません。式であるということは、「==」が「+」や「-」と同じような演算子であり、演算の結果、何らかの値が得られることでもあります。どういうことかというと、実際に対話モードでやってみます。

> a = 1⏎  ▹変数aの値を1にセットする
> a == 1⏎ ▹aの値は1と等しいか？ 
true       ▹真
> a == 2⏎ ▹aの値は2と等しいか？
false      ▹偽

「==」の結果はtrueとfalseとなっていることが分かります。そして、「==」の結果はtrueかfalseどちらかにしかなりません。決して0になったり1になったりしません。「==」は条件演算子と呼ばれます。条件演算子は他にもあります。

== 等しい
~= 等しくない
< 小さい
> 大きい
<= 小さいまたは等しい
>= 大きいまたは等しい

どれも演算の結果trueかfalseを返してきます。また対話モードで実験してみます。

> 1 == 1⏎
true
> 1 ~= 1⏎
false
> 1 ~= 2⏎
true
> 1 < 2⏎
true
> 1 < 1⏎
false
> 1 > 10⏎
false
> 1 > 0⏎
true
> 1 <= 1⏎
true
> 1 <= 0⏎
false
> 1 >= 1⏎
true
> 1 >= 2⏎
false

どれも直感的に理解しやすいものだと良いのですが、どうでしょう。色々試して感覚を掴むのが良いかと思います。

論理演算子については、いったんこのくらいにしておきます。 if文に戻ります。

if文の条件には論理演算子を使った式だけではなく、色々と置くことができます。しかし、最も基本的なものは、論理演算子を使った式の形をしていて、最も理解しやすいパターンだと言えます。

まず if 条件 then 実行したい文 end という形を覚えておきます。今回の問題を解くのに必要なのはそれだけです。

2.5 平方根を計算する方法

平方根を自力で計算するのはなかなか大変です。そこでLuaが用意していくれている機能を使います。どのようにLuaが用意してくれていて、どうやってそれを使えば良いかというと、関数というのが答えです。あらかじめLuaが用意されている関数を使うのは初めてではありません。何度も使っているprintも関数だし、前回使ったtonumberも関数です。関数は、今はやりませんが、自分で作ることもできます。用意された関数を利用するには、次のような形にします。

関数名(関数への引数1, 関数への引数2, 他にあれば続く…)

名前の後ろに括弧を付けて、引数を並べて括弧を閉じるのがポイントです。引数とは関数に渡す値、変数などです。ある関数がどのようなものを受け付けるかは、利用する関数に依ります。例えば、tonumber関数は文字列を受け付けて、それを数値に変換して結果を返してきます。

実はtonumber関数は文字列以外でも受け付けます。数値を引数として渡すと、その数値をそのまま返してきます。それ以外のものを渡した場合は、結果はnilになります。

print関数は何でも引数に受け付けます。 trueを渡した場合、画面にtrueと表示したり、数値を渡した場合、その数値を画面に表示して、当然文字列も受け付けて、その文字列を画面に表示します。このように何でも受け付ける関数というのは少数派でしょう。

関数にはその結果を戻り値として返してくるものがあります。 tonumber関数がそうでした。平方根を計算する関数もそうです。結果を返してくる関数を利用したということは、その結果を利用したいという状況がほとんどでしょう。結果を変数に保存できると便利です。その場合、次のように書きます。

変数名 = 関数名(関数への引数1, 関数への引数2, 他にあれば続く…)

こんな形で関数を呼び出すパターンは頻出します。

さて、Luaが用意してくれている平方根を求める関数はmath.sqrtという名前です。 sqrtというのは Square Root (平方根) のことです。ドット区切りになっていて奇妙に映るかもしれません。 mathというのは、関数をカテゴリに分類するために用意された名前だとみなすかと良いかもしれません。例えば、文字列を扱う関数はstringという名前の下に用意されていて、string.lenとかいった名前になっています。 mathには、他にもmath.sinといった関数や、math.piといった値が用意されています。

実はmathやstringというのはテーブルです。

奇妙な名前かもしれませんが、関数に違いはないので、printやtonumberと同じように使うことができます。対話モードで試してみましょう。

> math.sqrt(2)⏎
1.4142135623731 ▹ひとよひとよにひとみごろ
> math.sqrt(3)⏎
1.7320508075689 ▹ひとなみにおごれや
> math.sqrt(4)⏎
2.0
> math.sqrt(4.2)⏎
2.0493901531919

だいたい良い感じではないかと思います。しかし、注意しておきべきことがあります。

\(\sqrt{2}\)は無理数です。無理数は少数点以下の桁は無限に続いていきます。コンピューターが扱う数値には精度というものがあります。ひとつの数値を保持するのに、どのくらいビット幅を使うかというものです。精度があらかじめ決められているので、表現できる数値の範囲には限界があります。そのため、コンピューターが扱う浮動小数点数は、本当の意味で数学の実数とは異なります。このことが原因で問題が発生する場合もあれば、まったく表面化しない場合もあります。上の\(\sqrt{2}\)の場合、一見うまくいきます。 \(\sqrt{2} \times \sqrt{2}\)を計算してみましょう。

> math.sqrt(2) * math.sqrt(2)⏎
2.0

理想的な値になりました。しかし、毎回このような結果が得られるとは限らないことを片隅に置いておくと良いかと思います。

math.sqrt関数にはもう一つ限界があります。それは、負の値の平方根は求められないということです。

> math.sqrt(-1)⏎
-nan
> math.sqrt(-2)⏎
-nan

nanという値になりました。 nan は Not A Number (数値ではない) の意味です。 nanは特殊な数で、今のところこの数を使って何かすることはありません。ただ、だめなんだ、とだけ理解しておけば十分です。

math.sqrt関数に渡す引数を変数にしたり、返してきた値を変数に保存したりすることも、当然できます。

> x = 121⏎
> y = math.sqrt(x)⏎
> y⏎
11.0

だいたいこんなところです。

2.6 コードを書く

前準備はできたので、順番にやっていきます。

2.6.1 コマンドライン引数の取得

まずはコマンドラインから3つの引数を取得するところから手を付けていくことにします。コマンドラインで指定された引数を取得するには2つの方法があるのでした。

グローバル変数arg
... (3つのドット)

前回と同じように、今回もグローバル変数argを使うことにします。グローバル変数argは、テーブルであり、また配列でもあるのでした。 arg[0]には、コマンドラインで指定したプログラムのパスが入っています。そして、arg[1]、arg[2]、arg[3] … arg[n]と順番にコマンドライン引数が入っています。

前回もやったのですが、もう一度、実験して確認しておきましょう。次のような内容のファイルを作成します。

print(arg[0], arg[1], arg[2], arg[3], arg[4], arg[5])

このファイルの名前は qes.lua とでもしておきます(Quadratic Equation Solver という意味で名付けました)。

そして、コマンドラインで次のようにしてこのチャンクを実行してみます。

% lua54 qes.lua 1 2 3⏎
qes.lua	1	2	3	nil	nil

この実験の結果から、次のようになっていることが分かります。

arg[0] => qes.lua … 実行しているプログラム、すなわちファイルの名前
arg[1] => 1 … 1つ目のコマンドライン引数
arg[2] => 2 … 2つ目のコマンドライン引数
arg[3] => 3 … 3つ目のコマンドライン引数
arg[4] => nil … 指定しなかったため、無を意味するnilという値
arg[5] => nil … 指定しなかったため、無を意味するnilという値

無効な値であることを示すのにnilという値が取得できることが特徴的です。

他の多くの言語では、配列の有効な範囲を越えて値にアクセスすると、不快な動作をすることが多いです。 Luaでは単純にnilを返してきます。これは配列が真の配列ではなく、キーが数値であるテーブルから構成されているためでもあるのでしょう。

今回の問題で必要なのは最初の3つの引数です。それを変数で保持するようにしておきます。また、コマンドライン引数で取得した値は文字列なので、tonumberというのを利用して、数値に変換しておきます。前回はtonumberを使わずに、数値として解釈できる文字列なら、変換をせずともそのまま計算できることをやりました。対話モードで次のようにしてみます。

> "1" + "2"⏎
3.0

数値になっています。この特性を利用すればわざわざ数値に変換する必要はないように思えるかもしれません。しかし、数値であることが分かりきていて、また必須であるなら、数値にしておいた方が無難です。なので、次のようにして変換した数値を変数a、b、cに保持させます。

a = tonumber(arg[1])
b = tonumber(arg[2])
c = tonumber(arg[3])

a、b、cという名前は、それぞれ二次方程式の係数の名前と一致しているので、理解しやすいでしょう。

もし、コマンドライン引数が数値として解釈できない文字列であった場合どうなるでしょう。答は、nilになる、です。この動作を利用して、もしaがnilだったなら、コマンドライン引数が間違っているとif文で分岐して、エラー処理を行うことができます。今はエラー処理は無視しておきます。

2.6.2 計算をする

a、b、cの値が決まったので、解の式にそれを当てはめれば良いです。カンニングのために、もう一度解の式を書いておきます。

\(\large x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

問題では、実数解が2つの場合と、重解の場合と、実数解がない場合それぞれに対応しないといけないとなっています。どの場合に該当するかは、平方根の中の \(b^2 - 4ac\) を見れば良いのでした。この部分は 判別式 という呼び名がついています。英語では Discriminat というので D という文字があてがわれることが多いです。この慣習に従って、Luaで次のように書きます。

a = tonumber(arg[1])
b = tonumber(arg[2])
c = tonumber(arg[3])

D = b^2 - 4*a*c

Dが正か、0か、負の場合でif文を使って分岐…

べき乗の演算子「^」は初登場です。 b^2 は\(b^2\)の意味です。違和感があれば b*b と書いても構いません。

では、次が今回の最大の山場である、if文を書いていきます。

まず、Dが正の場合を書いてみましょう。前の解説では次のような形で紹介しました。

if 条件 then 条件が真のときに実行する文 end

この形でもいいのですが、改行をいれて読みやすくすることもできます。

if 条件 then
  条件が真のときに実行する文
end

この形式の方がよく使われるかと思います。なぜなら、実行する文が複数の場合、より見易いからです。

if 条件 then
  条件が真のときに実行する文1
  条件が真のときに実行する文2
  条件が真のときに実行する文3
  … 
end

条件が真のとき実行する文は、先頭に空白文字を入れて(インデントと言います)、頭を揃えておくのがミソです。空白の数は2つでなければならないということはありません。 3つ、4つ、でもOKです。ただし、一つのプログラムでは統一することが重要です。そうしなければ読み難いものになってしまいます。

最初のDが正のときの条件は D > 0 です。この条件が真なら、2つの実数解を求めて画面に表示します。ファイル qes.lua (Quadratic Equation Solverの意味) に次の内容を書きます。

a = tonumber(arg[1])
b = tonumber(arg[2])
c = tonumber(arg[3])

D = b^2 - 4*a*c

if D > 0 then
  x1 = (-b - math.sqrt(D)) / 2*a
  x2 = (-b + math.sqrt(D)) / 2*a
  print("x = " .. x1 .. ", " .. x2)
end

結果を表示するために使っているprint関数の引数で、「..」と書いています。これは省略の意味で書いたのではなく、実際のコードです。「..」は 連結演算子 (Concatenation Operator) と呼ばれます。 "Hello" .. "World" のように書くと "HelloWorld" という文字列が得られます。数値を文字列と連結することもできて "Hello" .. 42 とすると "Hello42" という文字列が得られます。変数でも連結できるし、「+」や「-」と同じように、複数回適用して一つの式とすることができます。

ここまで書いたら、一度動かしてみると良いです。

% lua qes.lua 1 1 -6⏎
x = -3.0, 2.0
% lua qes.lua 1 7 12⏎
x = -4.0, -3.0
% lua qes.lua 1 -7 12⏎
x = 3.0, 4.0

うまくいっているようで、続けて重解の場合を書いていきます。

a = tonumber(arg[1])
b = tonumber(arg[2])
c = tonumber(arg[3])

D = b^2 - 4*a*c

if D > 0 then
  x1 = (-b - math.sqrt(D)) / 2*a
  x2 = (-b + math.sqrt(D)) / 2*a
  print("x = " .. x1 .. ", " .. x2)
end

if D == 0 then
  x1 = -b / 2*a
  print("x = " .. x1)
end

もう一度動かしてみます。

% lua qes.lua 1 4 4⏎
x = -2.0
% lua qes.lua 1 -4 4⏎
x = 2.0

うまくいっているようです。続けて、実数解なしの場合を書いていきます。

一見うまくいっているように見えますが、厄介な問題も含んでいます。問題は D == 0 と浮動小数点数を比較しているところです。浮動小数点数の比較は一筋縄でいかないところがあります。よくとられる対策は、比較する2つの値の差が、非常に小さな数値(epsilonと呼ばれます)よりも小さいならば、だいたい等しいからOKとみなしてしまう方法です。しかし、どのような状況にでも対応できる完璧な解決策というのはありません。ここでは単純に無視して、素直に0と比較してしまっています。

次が最終形となります。

a = tonumber(arg[1])
b = tonumber(arg[2])
c = tonumber(arg[3])

D = b^2 - 4*a*c

if D > 0 then
  x1 = (-b - math.sqrt(D)) / 2*a
  x2 = (-b + math.sqrt(D)) / 2*a
  print("x = " .. x1 .. ", " .. x2)
end

if D == 0 then
  x1 = -b / 2*a
  print("x = " .. x1)
end

if D < 0 then
  print "no real solution"
end

これは簡単でした。動かしてみます。

% lua qes.lua 1 1 1⏎
no real solution
% lua qes.lua 1 2 5⏎
no real solution

うまくいっているようです。

あとはちゃんとテストをするべきなのですが、疲れてきたので今回はこれで完成としておきます。

2.6.3 残された課題

完成としたプログラムには大きな欠陥が一つあります。それは、aの値が0のときです。このとき、0で除算してしまっているため、おかしなことになります。 0による除算はよく知られたプログラミングのエラーです。

今のプログラムを0による除算を回避するように修正するのは簡単です。 if文を使ってaが0かどうか調べて、もし0ならプログラムを終了してしまえば良いです。

3 まとめ

今回はBMIの計算よりも、もうちょっと難しい数値計算にトライしてみました。最大の目玉はifによる条件分岐です。 ifはLuaでは日常的に使用する、基本的な、そして重要なパーツです。 ifにはまだ紹介していな部分があって、それは追い追い登場させることにします。

今回やったことはだたい以下の通りです。

コマンドライン引数の値を取得する方法
文字列から数値への変換
Luaが用意してくれている関数について
平方根を計算する関数 math.sqrt
論理演算子
ifの基本

前回からだいぶ間が空いてしまいました。次回はいつになるか分かりませんが、なるべき早く書きたいと思います。

Lua入門 その4 — 数値と計算と条件分岐

目次